【導讀】我保證這篇文章和你以前看過的所有文章都不同,這是 2012 年還在果殼的時候寫的,但是當時沒有來得及寫完就出國了……于是拖了兩年,嗯,我是拖延癥患者……這篇文章的核心思想就是:要讓讀者在不看任何數學公式的情況下理解傅里葉分析。
傅里葉分析不僅僅是一個數學工具,更是一種可以徹底顛覆一個人以前世界觀的思維模式。但不幸的是,傅里葉分析的公式看起來太復雜了,所以很多大一新生上來就懵圈并從此對它深惡痛絕。老實說,這么有意思的東西居然成了大學里的殺手課程,不得不歸咎于編教材的人實在是太嚴肅了。(您把教材寫得好玩一點會死嗎?會死嗎?)所以我一直想寫一個有意思的文章來解釋傅里葉分析,有可能的話高中生都能看懂的那種。所以,不管讀到這里的您從事何種工作,我保證您都能看懂,并且一定將體會到通過傅里葉分析看到世界另一個樣子時的快感。至于對于已經有一定基礎的朋友,也希望不要看到會的地方就急忙往后翻,仔細讀一定會有新的發現。
————以上是定場詩————
下面進入正題:
抱歉,還是要啰嗦一句:其實學習本來就不是易事,我寫這篇文章的初衷也是希望大家學習起來更加輕松,充滿樂趣。但是千萬!千萬不要把這篇文章收藏起來,或是存下地址,心里想著:以后有時間再看。這樣的例子太多了,也許幾年后你都沒有再打開這個頁面。無論如何,耐下心,讀下去。這篇文章要比讀課本要輕松、開心得多……
一、什么是頻域
從我們出生,我們看到的世界都以時間貫穿,股票的走勢、人的身高、汽車的軌跡都會隨著時間發生改變。這種以時間作為參照來觀察動態世界的方法我們稱其為時域分析。而我們也想當然的認為,世間萬物都在隨著時間不停的改變,并且永遠不會靜止下來。但如果我告訴你,用另一種方法來觀察世界的話,你會發現世界是永恒不變的,你會不會覺得我瘋了?我沒有瘋,這個靜止的世界就叫做頻域。
先舉一個公式上并非很恰當,但意義上再貼切不過的例子:
在你的理解中,一段音樂是什么呢?
這是我們對音樂最普遍的理解,一個隨著時間變化的震動。但我相信對于樂器小能手們來說,音樂更直觀的理解是這樣的:

好的!下課,同學們再見。
是的,其實這一段寫到這里已經可以結束了。上圖是音樂在時域的樣子,而下圖則是音樂在頻域的樣子。所以頻域這一概念對大家都從不陌生,只是從來沒意識到而已。
現在我們可以回過頭來重新看看一開始那句癡人說夢般的話:世界是永恒的。
將以上兩圖簡化:
時域:
頻域:

在時域,我們觀察到鋼琴的琴弦一會上一會下的擺動,就如同一支股票的走勢;而在頻域,只有那一個永恒的音符。
所以
你眼中看似落葉紛飛變化無常的世界,實際只是躺在上帝懷中一份早已譜好的樂章。
抱歉,這不是一句雞湯文,而是黑板上確鑿的公式:傅里葉同學告訴我們,任何周期函數,都可以看作是不同振幅,不同相位正弦波的疊加。在第一個例子里我們可以理解為,利用對不同琴鍵不同力度,不同時間點的敲擊,可以組合出任何一首樂曲。
而貫穿時域與頻域的方法之一,就是傳中說的傅里葉分析。傅里葉分析可分為傅里葉級數(Fourier Serie)和傅里葉變換(Fourier Transformation),我們從簡單的開始談起。
二、傅里葉級數(Fourier Series)的頻譜
還是舉個栗子并且有圖有真相才好理解。
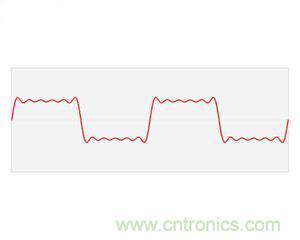
如果我說我能用前面說的正弦曲線波疊加出一個帶 90 度角的矩形波來,你會相信嗎?你不會,就像當年的我一樣。但是看看下圖:
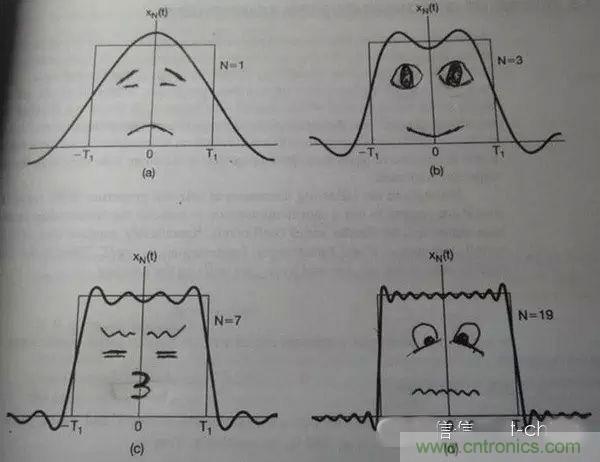
第一幅圖是一個郁悶的正弦波 cos(x)
第二幅圖是 2 個賣萌的正弦波的疊加
第三幅圖是 4 個發春的正弦波的疊加
第四幅圖是 10 個便秘的正弦波的疊加
隨著正弦波數量逐漸的增長,他們最終會疊加成一個標準的矩形,大家從中體會到了什么道理?
(只要努力,彎的都能掰直!)
隨著疊加的遞增,所有正弦波中上升的部分逐漸讓原本緩慢增加的曲線不斷變陡,而所有正弦波中下降的部分又抵消了上升到最高處時繼續上升的部分使其變為水平線。一個矩形就這么疊加而成了。但是要多少個正弦波疊加起來才能形成一個標準 90 度角的矩形波呢?不幸的告訴大家,答案是無窮多個。(上帝:我能讓你們猜著我?)不僅僅是矩形,你能想到的任何波形都是可以如此方法用正弦波疊加起來的。這是沒有接觸過傅里葉分析的人在直覺上的第一個難點,但是一旦接受了這樣的設定,游戲就開始有意思起來了。
還是上圖的正弦波累加成矩形波,我們換一個角度來看看:

在這幾幅圖中,最前面黑色的線就是所有正弦波疊加而成的總和,也就是越來越接近矩形波的那個圖形。而后面依不同顏色排列而成的正弦波就是組合為矩形波的各個分量。這些正弦波按照頻率從低到高從前向后排列開來,而每一個波的振幅都是不同的。一定有細心的讀者發現了,每兩個正弦波之間都還有一條直線,那并不是分割線,而是振幅為 0 的正弦波!也就是說,為了組成特殊的曲線,有些正弦波成分是不需要的。
這里,不同頻率的正弦波我們成為頻率分量。
好了,關鍵的地方來了!!
如果我們把第一個頻率最低的頻率分量看作“1”,我們就有了構建頻域的最基本單元。
對于我們最常見的有理數軸,數字“1”就是有理數軸的基本單元。
(好吧,數學稱法為——基。在那個年代,這個字還沒有其他奇怪的解釋,后面還有正交基這樣的詞匯我會說嗎?)時域的基本單元就是“1 秒”,如果我們將一個角頻率為w0的正弦波cos(w0t)看作基礎,那么頻域的基本單元就是w0。
有了“1”,還要有“0”才能構成世界,那么頻域的“0”是什么呢?cos(0t)就是一個周期無限長的正弦波,也就是一條直線!所以在頻域,0 頻率也被稱為直流分量,在傅里葉級數的疊加中,它僅僅影響全部波形相對于數軸整體向上或是向下而不改變波的形狀。
接下來,讓我們回到初中,回憶一下已經死去的八戒,啊不,已經死去的老師是怎么定義正弦波的吧。
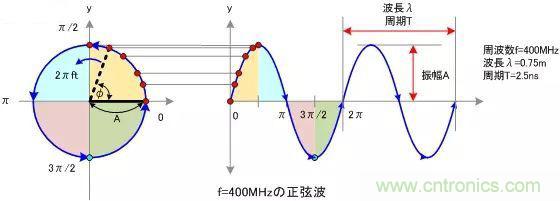
正弦波就是一個圓周運動在一條直線上的投影。所以頻域的基本單元也可以理解為一個始終在旋轉的圓以及這里:
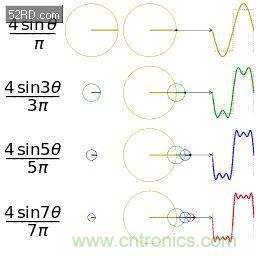
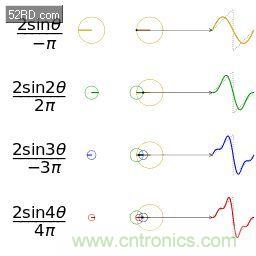
點出去的朋友不要被 wiki 拐跑了,wiki 寫的哪有這里的文章這么沒節操是不是。
介紹完了頻域的基本組成單元,我們就可以看一看一個矩形波,在頻域里的另一個模樣了:
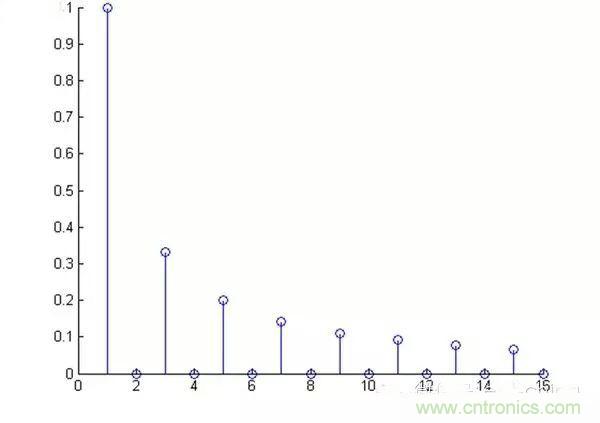
這是什么奇怪的東西?
這就是矩形波在頻域的樣子,是不是完全認不出來了?教科書一般就給到這里然后留給了讀者無窮的遐想,以及無窮的吐槽,其實教科書只要補一張圖就足夠了:頻域圖像,也就是俗稱的頻譜,就是——
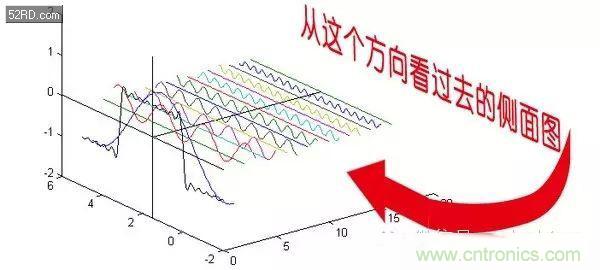
再清楚一點:
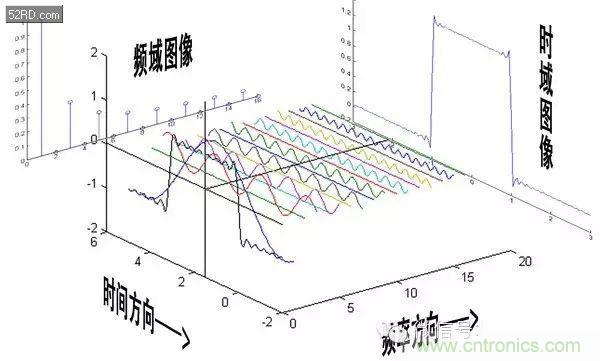
可以發現,在頻譜中,偶數項的振幅都是0,也就對應了圖中的彩色直線。振幅為 0 的正弦波。
老實說,在我學傅里葉變換時,維基的這個圖還沒有出現,那時我就想到了這種表達方法,而且,后面還會加入維基沒有表示出來的另一個譜——相位譜。
但是在講相位譜之前,我們先回顧一下剛剛的這個例子究竟意味著什么。記得前面說過的那句“世界是靜止的”嗎?估計好多人對這句話都已經吐槽半天了。想象一下,世界上每一個看似混亂的表象,實際都是一條時間軸上不規則的曲線,但實際這些曲線都是由這些無窮無盡的正弦波組成。我們看似不規律的事情反而是規律的正弦波在時域上的投影,而正弦波又是一個旋轉的圓在直線上的投影。那么你的腦海中會產生一個什么畫面呢?
我們眼中的世界就像皮影戲的大幕布,幕布的后面有無數的齒輪,大齒輪帶動小齒輪,小齒輪再帶動更小的。在最外面的小齒輪上有一個小人——那就是我們自己。我們只看到這個小人毫無規律的在幕布前表演,卻無法預測他下一步會去哪。而幕布后面的齒輪卻永遠一直那樣不停的旋轉,永不停歇。這樣說來有些宿命論的感覺。說實話,這種對人生的描繪是我一個朋友在我們都是高中生的時候感嘆的,當時想想似懂非懂,直到有一天我學到了傅里葉級數……
三、傅里葉級數(Fourier Series)的相位譜
上一章的關鍵詞是:從側面看。這一章的關鍵詞是:從下面看。
在這一章最開始,我想先回答很多人的一個問題:傅里葉分析究竟是干什么用的?這段相對比較枯燥,已經知道了的同學可以直接跳到下一個分割線。
先說一個最直接的用途。無論聽廣播還是看電視,我們一定對一個詞不陌生——頻道。頻道頻道,就是頻率的通道,不同的頻道就是將不同的頻率作為一個通道來進行信息傳輸。下面大家嘗試一件事:
先在紙上畫一個sin(x),不一定標準,意思差不多就行。不是很難吧。
好,接下去畫一個sin(3x)+sin(5x)的圖形。
別說標準不標準了,曲線什么時候上升什么時候下降你都不一定畫的對吧?
好,畫不出來不要緊,我把sin(3x)+sin(5x)的曲線給你,但是前提是你不知道這個曲線的方程式,現在需要你把sin(5x)給我從圖里拿出去,看看剩下的是什么。這基本是不可能做到的。
但是在頻域呢?則簡單的很,無非就是幾條豎線而已。
所以很多在時域看似不可能做到的數學操作,在頻域相反很容易。這就是需要傅里葉變換的地方。尤其是從某條曲線中去除一些特定的頻率成分,這在工程上稱為濾波,是信號處理最重要的概念之一,只有在頻域才能輕松的做到。
再說一個更重要,但是稍微復雜一點的用途——求解微分方程。(這段有點難度,看不懂的可以直接跳過這段)微分方程的重要性不用我過多介紹了。各行各業都用的到。但是求解微分方程卻是一件相當麻煩的事情。因為除了要計算加減乘除,還要計算微分積分。而傅里葉變換則可以讓微分和積分在頻域中變為乘法和除法,大學數學瞬間變小學算術有沒有。
傅里葉分析當然還有其他更重要的用途,我們隨著講隨著提。
————————————————————————————————————
下面我們繼續說相位譜:
通過時域到頻域的變換,我們得到了一個從側面看的頻譜,但是這個頻譜并沒有包含時域中全部的信息。因為頻譜只代表每一個對應的正弦波的振幅是多少,而沒有提到相位。基礎的正弦波A.sin(wt+θ)中,振幅,頻率,相位缺一不可,不同相位決定了波的位置,所以對于頻域分析,僅僅有頻譜(振幅譜)是不夠的,我們還需要一個相位譜。那么這個相位譜在哪呢?我們看下圖,這次為了避免圖片太混論,我們用7個波疊加的圖。
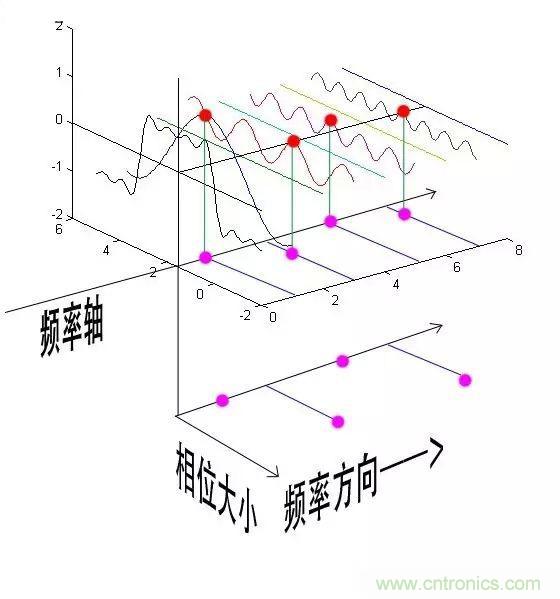
鑒于正弦波是周期的,我們需要設定一個用來標記正弦波位置的東西。在圖中就是那些小紅點。小紅點是距離頻率軸最近的波峰,而這個波峰所處的位置離頻率軸有多遠呢?為了看的更清楚,我們將紅色的點投影到下平面,投影點我們用粉色點來表示。當然,這些粉色的點只標注了波峰距離頻率軸的距離,并不是相位。
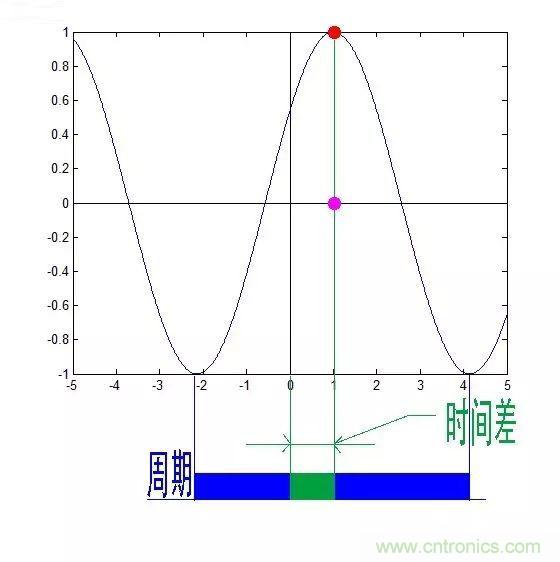
這里需要糾正一個概念:時間差并不是相位差。如果將全部周期看作2Pi或者360度的話,相位差則是時間差在一個周期中所占的比例。我們將時間差除周期再乘2Pi,就得到了相位差。
在完整的立體圖中,我們將投影得到的時間差依次除以所在頻率的周期,就得到了最下面的相位譜。所以,頻譜是從側面看,相位譜是從下面看。下次偷看女生裙底被發現的話,可以告訴她:“對不起,我只是想看看你的相位譜。”
注意到,相位譜中的相位除了0,就是Pi。因為cos(t+Pi)=-cos(t),所以實際上相位為Pi的波只是上下翻轉了而已。對于周期方波的傅里葉級數,這樣的相位譜已經是很簡單的了。另外值得注意的是,由于cos(t+2Pi)=cos(t),所以相位差是周期的,pi和3pi,5pi,7pi都是相同的相位。人為定義相位譜的值域為(-pi,pi],所以圖中的相位差均為Pi。
最后來一張大集合:
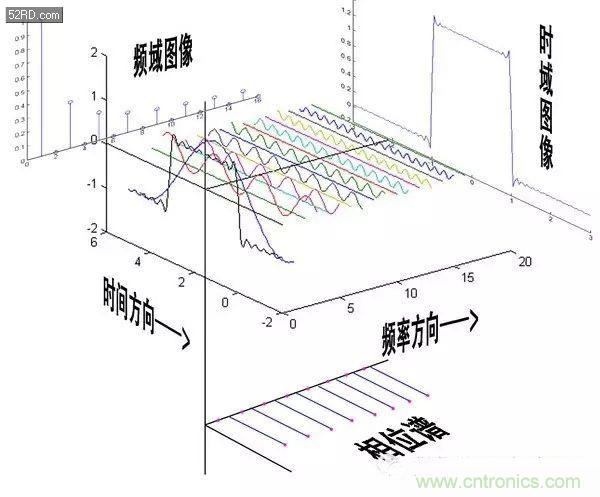
四、傅里葉變換(Fourier Tranformation)
相信通過前面三章,大家對頻域以及傅里葉級數都有了一個全新的認識。但是文章在一開始關于鋼琴琴譜的例子我曾說過,這個栗子是一個公式錯誤,但是概念典型的例子。所謂的公式錯誤在哪里呢?
傅里葉級數的本質是將一個周期的信號分解成無限多分開的(離散的)正弦波,但是宇宙似乎并不是周期的。曾經在學數字信號處理的時候寫過一首打油詩:
往昔連續非周期,
回憶周期不連續,
任你ZT、DFT,
還原不回去。
(請無視我渣一樣的文學水平……)
在這個世界上,有的事情一期一會,永不再來,并且時間始終不曾停息地將那些刻骨銘心的往昔連續的標記在時間點上。但是這些事情往往又成為了我們格外寶貴的回憶,在我們大腦里隔一段時間就會周期性的蹦出來一下,可惜這些回憶都是零散的片段,往往只有最幸福的回憶,而平淡的回憶則逐漸被我們忘卻。因為,往昔是一個連續的非周期信號,而回憶是一個周期離散信號。
是否有一種數學工具將連續非周期信號變換為周期離散信號呢?抱歉,真沒有。
比如傅里葉級數,在時域是一個周期且連續的函數,而在頻域是一個非周期離散的函數。這句話比較繞嘴,實在看著費事可以干脆回憶第一章的圖片。
而在我們接下去要講的傅里葉變換,則是將一個時域非周期的連續信號,轉換為一個在頻域非周期的連續信號。
算了,還是上一張圖方便大家理解吧:
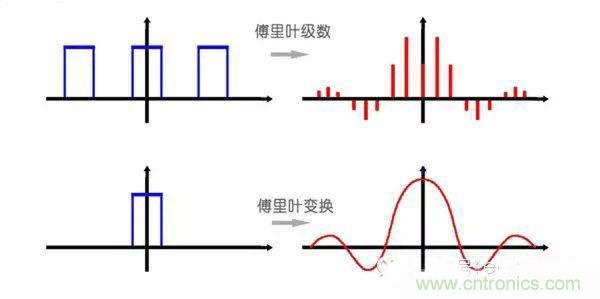
或者我們也可以換一個角度理解:傅里葉變換實際上是對一個周期無限大的函數進行傅里葉變換。
所以說,鋼琴譜其實并非一個連續的頻譜,而是很多在時間上離散的頻率,但是這樣的一個貼切的比喻真的是很難找出第二個來了。
因此在傅里葉變換在頻域上就從離散譜變成了連續譜。那么連續譜是什么樣子呢?
你見過大海么?
為了方便大家對比,我們這次從另一個角度來看頻譜,還是傅里葉級數中用到最多的那幅圖,我們從頻率較高的方向看。
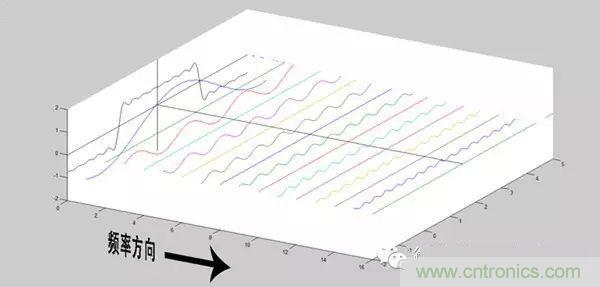
以上是離散譜,那么連續譜是什么樣子呢?
盡情的發揮你的想象,想象這些離散的正弦波離得越來越近,逐漸變得連續……直到變得像波濤起伏的大海:
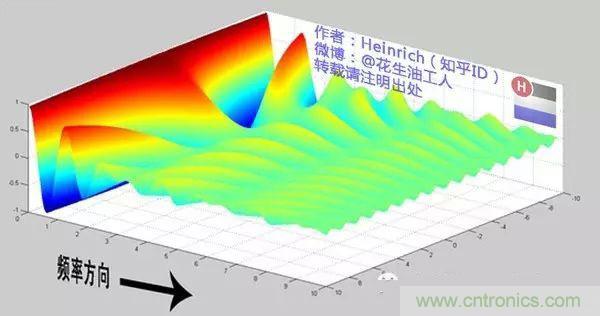
很抱歉,為了能讓這些波浪更清晰的看到,我沒有選用正確的計算參數,而是選擇了一些讓圖片更美觀的參數,不然這圖看起來就像屎一樣了。
不過通過這樣兩幅圖去比較,大家應該可以理解如何從離散譜變成了連續譜的了吧?原來離散譜的疊加,變成了連續譜的累積。所以在計算上也從求和符號變成了積分符號。
不過,這個故事還沒有講完,接下去,我保證讓你看到一幅比上圖更美麗壯觀的圖片,但是這里需要介紹到一個數學工具才能然故事繼續,這個工具就是——
五、宇宙耍帥第一公式:歐拉公式
虛數i這個概念大家在高中就接觸過,但那時我們只知道它是-1 的平方根,可是它真正的意義是什么呢
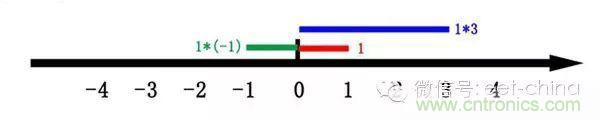
這里有一條數軸,在數軸上有一個紅色的線段,它的長度是1。當它乘以 3 的時候,它的長度發生了變化,變成了藍色的線段,而當它乘以-1 的時候,就變成了綠色的線段,或者說線段在數軸上圍繞原點旋轉了 180 度。
我們知道乘-1 其實就是乘了兩次 i 使線段旋轉了 180 度,那么乘一次 i 呢——答案很簡單——旋轉了 90 度。
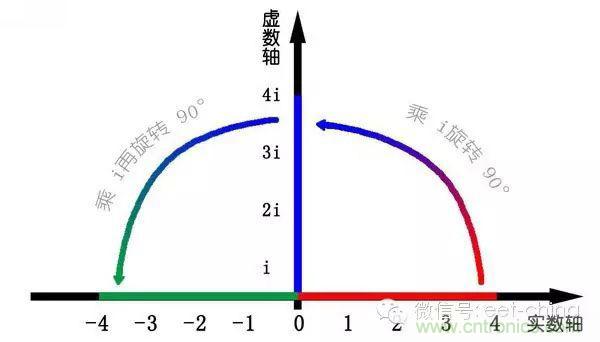
同時,我們獲得了一個垂直的虛數軸。實數軸與虛數軸共同構成了一個復數的平面,也稱復平面。這樣我們就了解到,乘虛數i的一個功能——旋轉。
現在,就有請宇宙第一耍帥公式歐拉公式隆重登場——這個公式在數學領域的意義要遠大于傅里葉分析,但是乘它為宇宙第一耍帥公式是因為它的特殊形式——當x等于 Pi 的時候。
經常有理工科的學生為了跟妹子表現自己的學術功底,用這個公式來給妹子解釋數學之美:”石榴姐你看,這個公式里既有自然底數e,自然數 1 和0,虛數i還有圓周率 pi,它是這么簡潔,這么美麗啊!“但是姑娘們心里往往只有一句話:”臭屌絲……“這個公式關鍵的作用,是將正弦波統一成了簡單的指數形式。我們來看看圖像上的涵義:
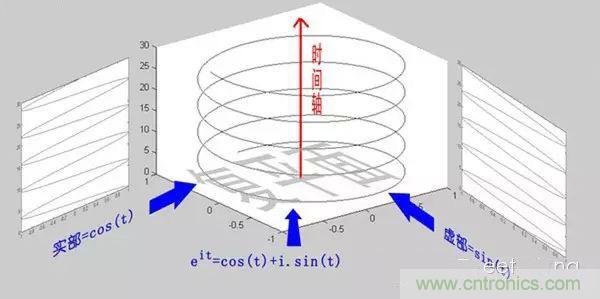
歐拉公式所描繪的,是一個隨著時間變化,在復平面上做圓周運動的點,隨著時間的改變,在時間軸上就成了一條螺旋線。如果只看它的實數部分,也就是螺旋線在左側的投影,就是一個最基礎的余弦函數。而右側的投影則是一個正弦函數。
關于復數更深的理解,大家可以參考:
復數的物理意義是什么?
這里不需要講的太復雜,足夠讓大家理解后面的內容就可以了。
六、指數形式的傅里葉變換
有了歐拉公式的幫助,我們便知道:正弦波的疊加,也可以理解為螺旋線的疊加在實數空間的投影。而螺旋線的疊加如果用一個形象的栗子來理解是什么呢?
光波
高中時我們就學過,自然光是由不同顏色的光疊加而成的,而最著名的實驗就是牛頓師傅的三棱鏡實驗:
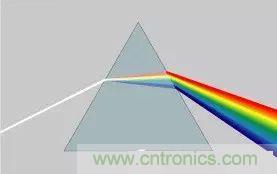
所以其實我們在很早就接觸到了光的頻譜,只是并沒有了解頻譜更重要的意義。
但不同的是,傅里葉變換出來的頻譜不僅僅是可見光這樣頻率范圍有限的疊加,而是頻率從 0 到無窮所有頻率的組合。
這里,我們可以用兩種方法來理解正弦波:
第一種前面已經講過了,就是螺旋線在實軸的投影。
另一種需要借助歐拉公式的另一種形式去理解:

將以上兩式相加再除2,得到:
這個式子可以怎么理解呢?
我們剛才講過,e^(it)可以理解為一條逆時針旋轉的螺旋線,那么e^(-it)則可以理解為一條順時針旋轉的螺旋線。而 cos (t)則是這兩條旋轉方向不同的螺旋線疊加的一半,因為這兩條螺旋線的虛數部分相互抵消掉了!
舉個例子的話,就是極化方向不同的兩束光波,磁場抵消,電場加倍。
這里,逆時針旋轉的我們稱為正頻率,而順時針旋轉的我們稱為負頻率(注意不是復頻率)。
好了,剛才我們已經看到了大海——連續的傅里葉變換頻譜,現在想一想,連續的螺旋線會是什么樣子:
想象一下再往下翻:
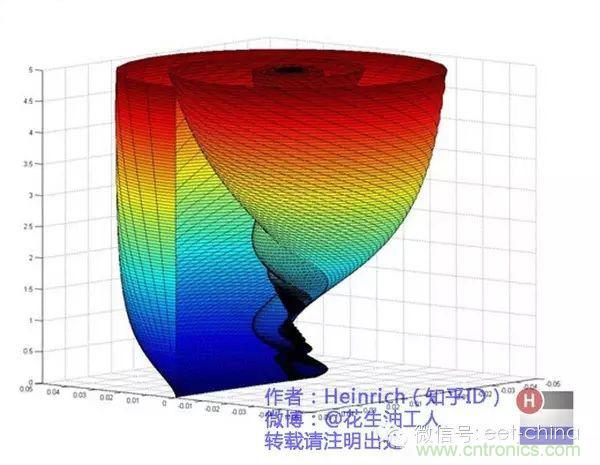
是不是很漂亮?
你猜猜,這個圖形在時域是什么樣子?
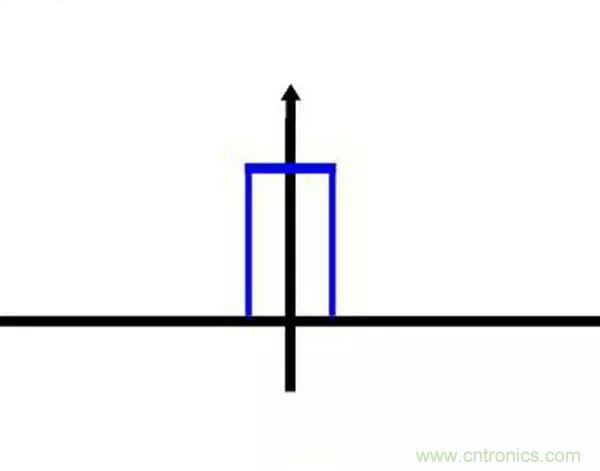
哈哈,是不是覺得被狠狠扇了一個耳光。數學就是這么一個把簡單的問題搞得很復雜的東西。
順便說一句,那個像大海螺一樣的圖,為了方便觀看,我僅僅展示了其中正頻率的部分,負頻率的部分沒有顯示出來。
如果你認真去看,海螺圖上的每一條螺旋線都是可以清楚的看到的,每一條螺旋線都有著不同的振幅(旋轉半徑),頻率(旋轉周期)以及相位。而將所有螺旋線連成平面,就是這幅海螺圖了。
好了,講到這里,相信大家對傅里葉變換以及傅里葉級數都有了一個形象的理解了,我們最后用一張圖來總結一下:
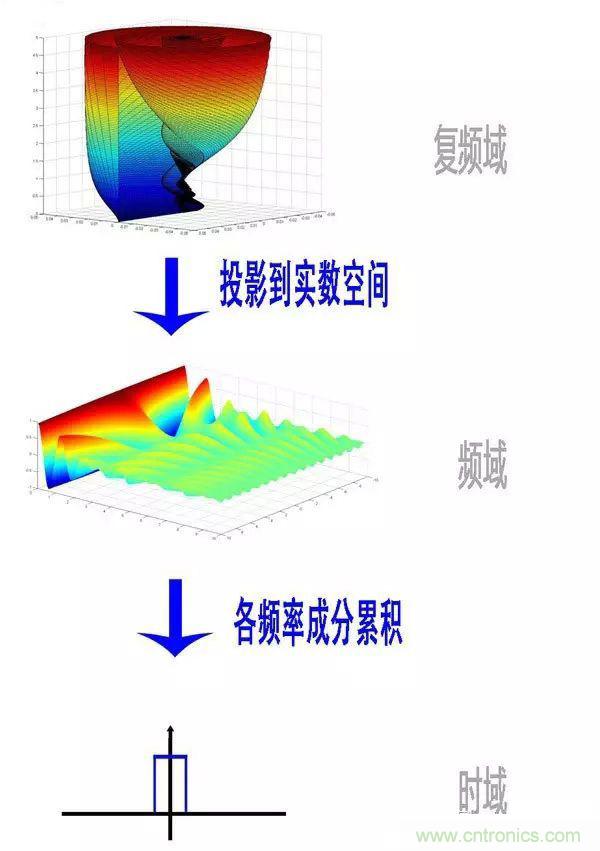
好了,傅里葉的故事終于講完了,下面來講講我的故事:
這篇文章第一次被卸下來的地方你們絕對猜不到在哪,是在一張高數考試的卷子上。當時為了刷分,我重修了高數(上),但是后來時間緊壓根沒復習,所以我就抱著裸考的心態去了考場。但是到了考場我突然意識到,無論如何我都不會比上次考的更好了,所以干脆寫一些自己對于數學的想法吧。于是用了一個小時左右的時間在試卷上洋洋灑灑寫了本文的第一草稿。
你們猜我的了多少分?
6分
沒錯,就是這個數字。而這 6 分的成績是因為最后我實在無聊,把選擇題全部填上了C,應該是中了兩道,得到了這寶貴的 6 分。說真的,我很希望那張卷子還在,但是應該不太可能了。
在重修的過程中,我仔細分析了每一個公式,試圖給這個公式以一個直觀的理解。雖然我知道對于研究數學的人來說,這樣的學習方法完全沒有前途可言,因為隨著概念愈加抽象,維度越來越高,這種圖像或者模型理解法將完全喪失作用。但是對于一個工科生來說,足夠了。
后來來了德國,這邊學校要求我重修信號與系統時,我徹底無語了。但是沒辦法,德國人有時對中國人就是有種藐視,覺得你的教育不靠譜。所以沒辦法,再來一遍吧。
這次,我考了滿分,而及格率只有一半。
老實說,數學工具對于工科生和對于理科生來說,意義是完全不同的。工科生只要理解了,會用,會查,就足夠了。但是很多高校卻將這些重要的數學課程教給數學系的老師去教。這樣就出現一個問題,數學老師講得天花亂墜,又是推理又是證明,但是學生心里就只有一句話:學這貨到底干嘛用的?
缺少了目標的教育是徹底的失敗。
在開始學習一門數學工具的時候,學生完全不知道這個工具的作用,現實涵義。而教材上有只有晦澀難懂,定語就二十幾個字的概念以及看了就眼暈的公式。能學出興趣來就怪了!
好在我很幸運,遇到了大連海事大學的吳楠老師。他的課全程來看是兩條線索,一條從上而下,一條從下而上。先將本門課程的意義,然后指出這門課程中會遇到哪樣的問題,讓學生知道自己學習的某種知識在現實中扮演的角色。然后再從基礎講起,梳理知識樹,直到延伸到另一條線索中提出的問題,完美的銜接在一起!
這樣的教學模式,我想才是大學里應該出現的。
最后,寫給所有給我點贊并留言的同學。真的謝謝大家的支持,也很抱歉不能一一回復。因為知乎專欄的留言要逐次加載,為了看到最后一條要點很多次加載。當然我都堅持看完了,只是沒辦法一一回復。
本文只是介紹了一種對傅里葉分析新穎的理解方法,對于求學,還是要踏踏實實弄清楚公式和概念,學習,真的沒有捷徑。但至少通過本文,我希望可以讓這條漫長的路變得有意思一些。




